Tutto sulla Forza di Coriolis: gli aspetti matematici

Tutto sulla Forza di Coriolis: gli aspetti matematici

Nell'articolo "Tutto sulla forza di Coriolis: vortici, gravi ed esposizione divulgativa" abbiamo affrontato l'argomento in modo descrittivo, per capirne i meccanismi che la provocano. Qui daremo invece una dimostrazione matematica e quindi più rigorosa degli effetti di questa forza, corredando il tutto da qualche esercizio esplicativo. In questo articolo è necessaria la conoscenza del calcolo vettoriale, perché l'esposizione matematica richiede necessariamente l'uso di vettori e trigonometria, che descrivono posizioni, velocità e accelerazioni non solo in termini puramente numerici (detti scalari) ma anche in termini di posizione/direzione. Per esprimere le quantità vettoriali e distinguerle da quelle puramente numeriche, nelle formule utilizzeremo il grassetto.

Ora, quando si cerca di esprimere il moto assoluto (rispetto cioè a un sistema di riferimento inerziale) di un punto materiale attraverso un sistema di riferimento non inerziale, si dimostra il cosiddetto Teorema dei Moti Relativi, ovvero Va = Vr + VT: la velocità assoluta di un punto è uguale alla velocità relativa di quel punto (rispetto cioè al riferimento non inerziale) più la velocità (chiamata di trascinamento) del sistema non inerziale stesso rispetto a quello inerziale (che è fisso) in corrispondenza dello stesso punto.

Nell'andare a determinare le accelerazioni (derivate delle velocità) che ne emergono, spuntano fuori dei termini che esprimono l'esistenza di accelerazioni (e quindi di forze) aggiuntive. Tra queste appare l'accelerazione di Coriolis che è data dal prodotto (vettoriale) tra la velocità angolare della Terra e la velocità del corpo in movimento rispetto alla Terra nel punto considerato, nella forma seguente:

Come abbiamo visto nell'altro articolo citato sopra, essa si genera quando il corpo, spostandosi, si porta in zone dove il sistema di riferimento rotante, pur avendo velocità angolare costante, varia la sua velocità lineare (perché cambia la distanza dal centro o dall'asse di rotazione). Naturalmente la Forza di Coriolis sarà data poi semplicemente moltiplicando l'accelerazione di Coriolis per la massa del corpo (seconda legge della dinamica di Newton).

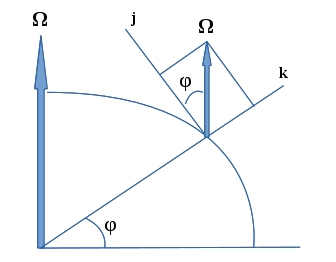Le componenti dei vettori sono calcolate rispetto alle 3 direzioni ovest-est (direzione i, perpendicolare alla figura), sud-nord (direzione j) e quota (direzione k), con tale terna centrata sul punto in movimento. Da semplici considerazioni trigonometriche si vede che la velocità angolare della Terra ha pertanto componenti Ω = (0, Ωcosφ, Ωsinφ), dove φ = latitudine. Invece le componenti della velocità del corpo nelle 3 direzioni i,j e k le chiameremo rispettivamente V = (u,v,z). Ora, la chiave per vedere come funziona l'accelerazione (e quindi la forza) di Coriolis è quella di sviluppare il prodotto vettoriale, il che corrisponde a calcolare la seguente matrice: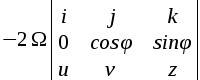

Il prodotto vettoriale in sé già ci dice che l'accelerazione di Coriolis è un vettore perpendicolare al piano formato dai vettori Ω e V. Ma lo sviluppo del calcolo ci permette di individuare le sue singole componenti nelle 3 direzioni spaziali (con cardine nel punto considerato, che ruota insieme alla Terra, il nostro sistema "mobile", non inerziale) e studiare così gli effetti pratici della forza che ne consegue. Lo sviluppo della matrice porta alla seguente formula nelle 3 componenti i, j e k del vettore accelerazione:


Come si può osservare, in generale l'accelerazione di Coriolis si manifesta in tutte e tre le direzioni dello spazio, in dipendenza dalla latitudine e dalla velocità e direzione del corpo in movimento. In particolare osserviamo come la componente ovest-est dell'accelerazione di Coriolis dipenda dalle componenti v e z della velocità del corpo, quindi dalle componenti lungo sud-nord e lungo la quota, mentre le altre due componenti solo dalla componente ovest-est. Per illustrare meglio quello che può succedere esaminiamo alcuni casi particolari.

La locomotiva

Ci troviamo nell'emisfero nord e abbiamo una locomotiva che viaggia lungo un parallelo, quindi esattamente in direzione est-ovest, o ovest-est. La velocità del nostro "corpo" avrà allora solo una componente e scriveremo che V = (u,0,0). In questo caso abbiamo:


Dunque ci sarà una deviazione verso destra (verso nord o sud secondo se la locomotiva viaggia verso ovest o est rispettivamente) con una forza pari a F = 2mΩu sinφ, dove m è la massa della locomotiva. Abbiamo una forza anche lungo la verticale (componente lungo k) pari a F = 2mΩu cosφ, verso l'alto se si viaggia verso est, verso il basso se si viaggia verso ovest. Ovviamente in realtà la locomotiva non devia da nessuna parte perché è vincolata ai binari, tuttavia i binari questa forza la subiscono...

Caduta dei gravi

Stavolta V = (0,0,-z) in quanto nella caduta ovviamente non ci stiamo spostando nelle altre due direzioni. Il segno (-) è perché il corpo va verso il basso, mentre abbiamo definito come positiva la direzione verso l'alto. In questo caso abbiamo:


Come avevamo già detto nell'articolo divulgativo, i gravi in caduta libera subiscono una deviazione verso est! Proviamo a fare un esempio numerico, supponendo che il corpo cada da una quota di 5000 metri. Sappiamo che se il grave parte da fermo allora z = gt, con g = 9.81 m/s2 (accelerazione di gravità) e t è il tempo espresso in secondi. Il tempo di caduta da un'altezza h è pari a t = (2h/g)1/2 (trascurando l'attrito dell'aria). Così se h = 5000 metri otteniamo un tempo di caduta t = 31.93 s. Integrando ac da 0 a t otteniamo la velocità di Coriolis vc = Ωgt2 cosφ. Integrando ancora sempre da 0 a t abbiamo finalmente lo spostamento (che già sappiamo essere verso est) sc = 1/3 Ωgt3 cosφ. Sostituendo i dati e ipotizzando di trovarci all'equatore (dove φ = 0) otteniamo circa 7.8 m.

Nei pressi dell'equatore

Spesso si sente dire che la Forza di Coriolis si annulla all'equatore ed è comunque molto debole nei pressi dello stesso. Questo non è completamente vero, ma lo diventa sotto certe ipotesi e punti di vista. Infatti, dalla formula generale vediamo che se siamo all'equatore, allora φ = 0 e quindi sinφ = 0 e cosφ = 1. Sostituendo si ha:

ac = -2Ω x V = i (-2Ωz) + k (2Ωu)

Come si vede all'equatore l'accelerazione di Coriolis ha ancora 2 componenti, una lungo la verticale (come abbiamo visto nel caso della caduta dei gravi) e l'altra lungo i paralleli. Tuttavia quando si parla di cicloni e anticicloni, il movimento prevalente delle masse d'aria al livello di sistema è sul piano orizzontale per cui z = 0. Di conseguenza resta ac = k (2Ωu), cioè non abbiamo più deviazioni sul piano orizzontale stesso e quindi l'aria non è più in grado di invorticarsi. Per questo motivo non si hanno vortici all'equatore ed essi fanno molta fatica a formarsi vicino all'equatore. Quando si forma una perturbazione in queste zone essa può acquisire un moto vorticoso sempre più evidente e importante mano a mano che la perturbazione stessa si allontana dall'equatore (vedi la formazione di cicloni tropicali, uragani e tifoni...)

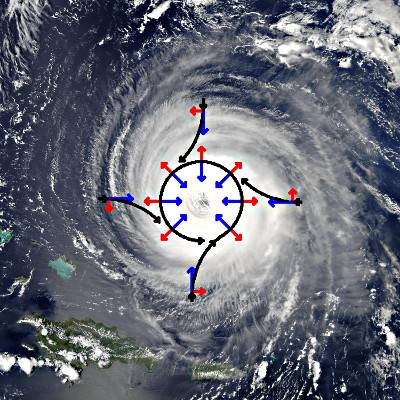
Nella foto in alto l'uragano Isabel con lo schema del vortice causato dalla Forza di Coriolis.