L'indice di Scharlau per il disagio climatico
L'indice di Scharlau per il disagio climatico
 Per via sperimentale, senza considerare il vento, Scharlau ha messo in relazione la temperatura limite dell’aria (rispetto all’umidità atmosferica) oltre la quale l’organismo di un uomo medio e in salute accusa disagio.
Per via sperimentale, senza considerare il vento, Scharlau ha messo in relazione la temperatura limite dell’aria (rispetto all’umidità atmosferica) oltre la quale l’organismo di un uomo medio e in salute accusa disagio.
I valori così trovati, se tracciati su un grafico, danno luogo alla cosiddetta "curva di Scharlau". I dati meteorologici considerati sono pertanto solamente:
1)l’umidità relativa (%);
2)la temperatura dell’aria (°C).
L'autore, tuttavia, ha realizzato due diverse tabelle, specifiche per le principali stagioni, ovvero una che riguarda il disagio climatico invernale e l’altra quello estivo.
Combinando umidità relativa e temperatura Scharlau ha determinato il disagio fisiologico come segue: come indicato nella tabella, nel caso invernale abbiamo i valori limite umidità-temperatura per le condizioni ambientali di freddo-umido in assenza di vento.
Tabella dunque valida per il disagio climatico invernale, vale a dire in condizioni di freddo-umido.
Precisamente, per ogni valore di umidità relativa, si trova la temperatura dell’aria di sotto al quale, senza vento, l’organismo prova disagio.
L’Indice di Scharlau per il disagio invernale è valido però solamente per UR > 40% ed è sensibile soprattutto tra -6°C e 5°C.
Al di fuori di questi limiti, a prescindere dai valori dell'umidità, l’indice attribuisce in ogni caso "benessere" per temperature > 5°C e "disagio intenso" per temperature < -6°C.
Indice di Scharlau invernale
UR(%) | 90 | 85 | 80 | 75 | 70 | 65 | 60 | 55 | 50 | 45 | 40 | |
Tc(°C) | 3.5 | 2.8 | 2.2 | 1.8 | 1.5 | 0.5 | 0.0 | - 0.3 | - 0.5 | - 1.5 | - 2.5 | |
Questa è l'equazione che genera la tabella, utile in caso di automatismi e per calcolare eventuali valori intermedi:
dove UR = umidità relativa (%), T = temperatura. La temperatura critica Tc è il valore di T che determina IS = 0 in funzione di UR.
Quando la differenza tra la temperatura reale T (rilevata da una stazione meteo) e quella critica Tc è:
- positiva: allora la temperatura rilevata è maggiore della temperatura critica --> niente disagio;
- negativa: allora la temperatura rilevata è inferiore quella critica --> si ha disagio (debole, moderato o intenso, secondo l'entità della differenza.
Indice di Scharlau estivo
UR(%) | 100 | 95 | 90 | 85 | 80 | 75 | 70 | 65 | 60 | 55 | 50 | 45 | 40 | 35 | 30 | |
Tc(°C) | 15.5 | 17.3 | 18.2 | 19.1 | 20.1 | 21.1 | 22.2 | 23.4 | 24.8 | 25.2 | 28.0 | 30.1 | 32.2 | 34.8 | 35.5 | |
Come detto esiste anche un indice di Scharlau valido per l'estate. Per ogni valore di RH, vi è la temperatura oltre la quale non c'è più uno stato di benessere, entrando così nelle tipiche condizioni di caldo umido.
In questo caso l'indice vale per valori di umidità relativa > 30% e l'intervallo di temperatura tipico è compreso tra 17°C e 39°C. Al di fuori di questi estremi, anche se variamo l’umidità relativa, l’indice attribuisce comunque "benessere" per temperature < 17°C e "disagio intenso" per quelle > 39°C.
Come fatto in precedenza anche in questo caso vale un'equazione, che stavolta è logaritmica (in base n):
dove UR = umidità relativa (%), T = temperatura. La temperatura critica Tc è il valore di T che determina IS = 0, sempre in funzione di UR. Anche in questo caso la differenza tra la temperatura veramente rilevata dalla stazione meteo T, e la temperatura critica Tc, dà luogo a un "gradiente" che può essere:
- positivo: la temperatura rilevata non supera la temperatura critica --> no disagio;
- negativo: la temperatura rilevata supera la temperatura critica --> disagio, tanto più intenso quanto maggiore è la differenza stessa.
CLASSE INDICE SCHARLAU (IS) | DESCRIZIONE | ||||
IS ≥ 0 | Benessere | ||||
- 1 < IS < 0 | Disagio debole | ||||
- 3 < IS ≤ - 1 | Disagio moderato | ||||
IS ≤ - 3 | Disagio intenso | ||||
Per entrambi i casi (estivo o invernale che sia), si hanno delle soglie di disagio, date dal valore di IS calcolato. La descrizione è riportata nella tabella qui sopra.
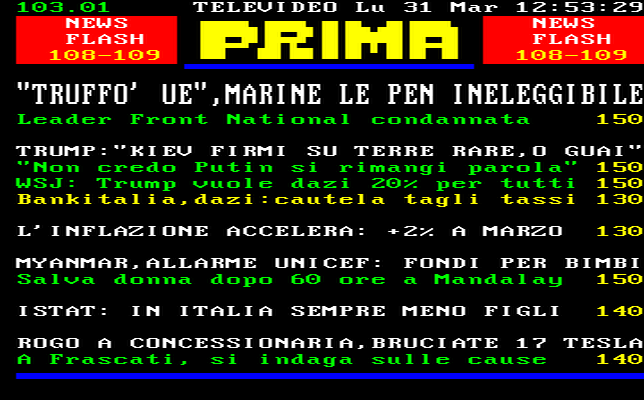
Nella figura che apre l'articolo (tratta da meteoBelluzzi, http://studenti.scuole.bo.it/meteo2/scharlau.php), invece, l’area verde indica la zona di benessere, quelle aree azzurre e blu un disagio debole, moderato o intenso durante l'inverno, mentre le aree arancione e rosse indicano un disagio debole, moderato o intenso per quanto riguarda il periodo estivo. Infine, dove si incrociano una qualunque retta orizzontale passante per i valori di UR e una qualunque retta verticale passante per i valori di T, determina in quale area cade la percezione di benessere o disagio secondo la formula di Scharlau.