Previsioni Meteo giuste o sbagliate... in che senso? La verifica delle performances

Previsioni Meteo giuste o sbagliate... in che senso? La verifica delle performances

Supponiamo che stia piovendo a Roma Nord, mentre a Roma Sud c'è Sole (succede più spesso di quanto si immagini). A Roma sta piovendo o no? Come vedete non è facile rispondere a questa domanda, perché dipende da quale parte della città vi trovate. Ecco, figuriamoci se possa avere un senso chiedere se a Roma pioverà! Occorre allora definire cosa si intende per evento previsto e trovare un metodo oggettivo per verificare tale previsione. Il concetto di per sé è semplice: la verifica delle previsioni meteorologiche consiste essenzialmente nell'esaminarne l'attendibilità attraverso il confronto tra le osservazioni (dati misurati da stazioni meteorologiche, immagini satellitari e derivati dai radar) e le previsioni fatte. Questo è importante per migliorare il proprio lavoro di previsore e tutta la ricerca tecnico-scientifica in materia. Può capitare ad esempio di individuare qualche errore sistematico per un'area specifica e questo consente di applicare locali fattori correttivi.

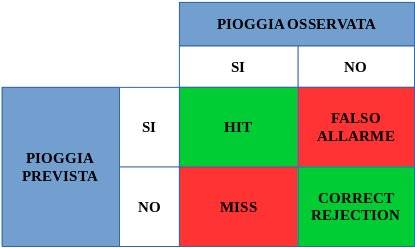
Indubbiamente il parametro per eccellezza sottoposto a verifica è la precipitazione. Esistono diversi metodi e tecniche per verificare l’affidabilità delle previsioni le cui linee guida sono dettate dal WMO (World Meteorological Organization). Per la pioggia il metodo utilizzato ad esempio dal Lamma Toscana è quello descritto dalla tabella in figura, detta "tabella di contingenza". E' utilizzata in statistica per rappresentare e analizzare le relazioni tra due o più variabili e la loro frequenza relativa. La tabella riassume le 4 combinazioni possibili delle coppie "previsioni-osservazioni" relativamente alla precipitazione di un determinato periodo su una determinata zona. In particolare, essendoci solo due stati possibili (PIOGGIA SI o PIOGGIA NO) abbiamo 4 eventi totali possibili di cui 2 piovosi e 2 non piovosi e precisamente:

A) HIT (o previsione corretta) = numero di volte in cui l’evento è stato previsto e osservato, cioè si prevedeva pioggia ed effettivamente ha piovuto;
B) FALSO ALLARME = numero di volte in cui l’evento è stato previsto, ma non osservato, cioè era stata prevista pioggia, ma non ha piovuto;
C) MISS (o previsione mancata) = numero di volte in cui l’evento è stato osservato, ma non era previsto, cioè ha piovuto, ma non era stato previsto;
D) CORRECT REJECTION = numero di volte in cui l’evento non è stato né previsto né osservato, cioè non ha piovuto e in effetti non era prevista pioggia.

Come si fa a stabilire in modo oggettivo e sistematico se ha piovuto o no? Bastano 4 gocce? Deve diluviare? Innanzitutto occorre uno strumento di misura, per esempio il pluviometro. Ma occorre sapere che è necessario stabilire una soglia per escludere l’attribuzione di pioggia a fenomeni di condensazione dovuti, per esempio, alla presenza di nebbia o alla formazione di rugiada. Una scelta sensata può essere quella di 0,6 mm per esempio. Ma i pluviometri misurano la pioggia solo dove si trovano. Se sono troppo distanti come faccio a sapere se ha piovuto, nella zona di interesse, in punti non misurati? Occorre che esista una rete sufficientemente "ricca" di stazioni e, sempre al Lamma, è stato adottato come criterio univoco per stabilire se la pioggia si è effettivamente verificata se almeno il 20% dei pluviometri presenti nell’area geografica sottoposta a verifica ha mediamente registrato almeno 0,6 mm negli intervalli temporali considerati (mattina, pomeriggio e sera). Sono tutte cose da definire bene, capite che prevedere pioggia entro le prossime 72 ore non è lo stesso che prevederla dalle 15 alle 20 di domani...

Una volta stabiliti i criteri di verifica, si procede con la raccolta delle informazioni. Ad A, B, C, D si associa il valore "1" se l'evento in questione si verifica, "0" altrimenti. Essendo mutuamente escludentesi se uno dei 4 vale 1, gli altri 3 varranno necessariamente 0. I parametri statistici utilizzati per interpretare i risultati in genere sono:
- Accuracy = (A+D)/(A+B+C+D). Determina la frazione di previsioni corrette rispetto al totale delle previsioni (sia di pioggia che di non pioggia) ed è fortemente influenzato dal tipo di evento più comune (di solito "pioggia NO"). Il risultato è "0" (previsione errata) oppure "1" (previsione corretta).
- Probability of Detection (POD) = A/(A+C). E' la percentuale di volte in cui la pioggia è stata prevista correttamente rispetto a tutte le volte che è piovuto. Cioè, su tutte le volte che ha piovuto quante volte è stata prevista pioggia correttamente? Anche qui si ha "0" (previsione errata) oppure "1" (previsione corretta), ma attenzione: siccome questo indice non considera i falsi allarmi, va letto congiuntamente all’indice FAR. Infatti, se ad esempio prevedessimo sempre pioggia, avremmo un POD molto buono (addirittura pari a 1 o 100%), ma allo stesso tempo un FAR altissimo.
- False Alarm ratio (FAR) = B/(A+B). E' la percentuale di volte in cui è stata prevista la pioggia, ma non si è verificata rispetto al totale di volte in cui è stata prevista pioggia. Ovvero, quante volte abbiamo previsto pioggia e invece non ha piovuto? Il risultato è "0" (previsione errata) oppure "1" (previsione corretta).
- BIAS = (A+B)/(A+C). E' il rapporto tra il numero degli eventi di pioggia previsti e il numero di eventi di pioggia effettivamente osservati; fornisce quindi indicazioni sulla tendenza a sovrastimare (BIAS > 1) o sottostimare (BIAS < 1) il numero di eventi di pioggia.

I risultati della verifica si ritengono soddisfacenti se, congiuntamente, POD > 0.6, FAR < 0.4, ACCURACY > 0.8 e BIAS è compreso tra 0.8 e 1.2.

Osservazione: può sembrare strano, ma siccome il metodo può essere influenzato in modo significativo dalla percentuale di eventi piovosi rispetto al totale degli eventi in genere risulta che meno piove nell’arco temporale considerato, minori sono le performance della verifica. In primavera, ma specialmente in estate in cui, non solo piove molto meno, ma le precipitazioni sono spesso legate a fenomeni per loro natura meno predicibili e meno estesi geograficamente, per esempio i temporali.

Fonti: Lamma, Centrometeo